2019年普通高等学校招生全国统一考试
理科数学
本试题共5页。考试结束后,将本试题和答卷卡一并交回。
需要注意的地方:
1.答卷前,考生先将我们的名字、准考证号码填写了解,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题需要用2B铅笔填涂;非选择题需要用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹了解。
3.请根据题号顺序在答卷卡各题目的答卷地区内作答,超出答卷地区书写的答案无效;在草稿纸、试题上答卷无效。
4.作图可先用铅笔画出,确定后需要用黑色字迹的签字笔描黑。
5.维持卡面清洗,不要折叠,不要弄破、弄皱,不准用涂改液、修正带、刮纸刀。
1、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目需要的.
1.设集合A={x|x2-5x+6>0},B={ x|x-1<0},则A∩B=
A. B.
C. D.
2.设z=-3+2i,则在复平面内![]() 对应的点坐落于
对应的点坐落于
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.已知![]() =,
=,![]() =,
=,![]() =1,则
=1,则![]() =
=
A.-3 B.-2
C.2 D.3
4.2019年1月3日嫦娥四号探测器成功达成人类历史上初次月球背面软着陆,国内航天事业获得又一重大收获,达成月球背面软着陆需要解决的一个重点技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,坐落于地月连线的延长线上.设地球水平为M1,月球水平为M2,地月距离为R,
点是平衡点,坐落于地月连线的延长线上.设地球水平为M1,月球水平为M2,地月距离为R,![]() 点到月球的距离为r,依据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,依据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,因为
,因为![]() 的值非常小,因此在近似计算中
的值非常小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.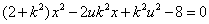 B.
B.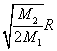
C.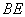 D.
D.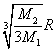
5.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特点是
A.中位数 B.平均数
C.方差 D.极差
6.若a>b,则
A.ln>0 B.3a<3b
C.a3−b3>0 D.│a│>│b│
7.设α,β为两个平面,则α∥β的充要条件是
A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行
C.α,β平行于同一条直线 D.α,β垂直于同一平面
8.若抛物线y2=2px的焦点是椭圆![]() 的一个焦点,则p=
的一个焦点,则p=
A.2 B.3
C.4 D.8
9.下列函数中,以![]() 为周期且在区间单调递增的是
为周期且在区间单调递增的是
A.f=│cosplay 2x│ B.f=│sin 2x│
C.f=cosplay│x│ D.f= sin│x│
10.已知α∈,2sin 2α=cosplay 2α+1,则sin α=
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.设F为双曲线C:![]() 的右焦点,
的右焦点,![]() 为坐标原点,以
为坐标原点,以![]() 为直径的圆与圆
为直径的圆与圆![]() 交于P,Q两点.若
交于P,Q两点.若![]() ,则C的离心率为
,则C的离心率为
A.![]() B.
B.![]()
C.2 D.![]()
12.设函数![]() 的概念域为R,满足
的概念域为R,满足![]() ,且当
,且当![]() 时,
时,![]() .若对任意
.若对任意![]() ,都有
,都有![]() ,则m的取值范围是
,则m的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2、填空题:本题共4小题,每小题5分,共20分.
13.国内高铁飞速发展,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为__________.
14.已知![]() 是奇函数,且当
是奇函数,且当![]() 时,
时,![]() .若
.若![]() ,则
,则![]() __________.
__________.
15.![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() .若
.若![]() ,则
,则![]() 的面积为__________.
的面积为__________.
16.中国有悠久的金石文化,印信是金石文化的代表之1、印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)

3、解答卷:共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考试试题,每一个考试试题考生都需要作答.第22、23为选考试试题,考生依据需要作答.
(一)必考试试题:共60分。
17.(12分)
如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
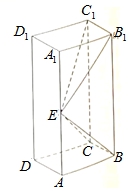
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
18.(12分)
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
19.(12分)
已知数列{an}和{bn}满足a1=1,b1=0,![]() ,
,![]() .
.
(1)证明:{an+bn}是等比数列,{an–bn}是等差数列;
(2)求{an}和{bn}的通项公式.
20.(12分)
已知函数![]() .
.
(1)讨论f的单调性,并证明f有且仅有两个零点;
(2)设x0是f的一个零点,证明曲线y=ln x 在点A处的切线也是曲线![]() 的切线.
的切线.
21.(12分)
已知点A,B,动点M满足直线AM与BM的斜率之积为−![]() .记M的轨迹为曲线C.
.记M的轨迹为曲线C.
(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连结QE并延长交C于点G.
(i)证明:![]() 是直角三角形;
是直角三角形;
(ii)求![]() 面积的最大值.
面积的最大值.
(二)选考试试题:共10分.请考生在第22、23题中任选一题作答。假如多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在极坐标系中,O为极点,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与
且与![]() 垂直,垂足为P.
垂直,垂足为P.
(1)当![]() 时,求
时,求![]() 及l的极坐标方程;
及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
23.[选修4-5:不等式选讲](10分)
已知![]()
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
2019年普通高等学校招生全国统一考试
理科数学·参考答案
1.A 2.C 3.C 4.D 5.A
6.C 7.B 8.D 9.A 10.B
11.A 12.B
13.0.98 14.–3
15.6![]() 16.26;
16.26;![]()
17.解:(1)由已知得,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]()
![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)知![]() .由题设知
.由题设知![]() ,所以
,所以![]() ,
,
故![]() ,
,![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 的方向为x轴正方向,
的方向为x轴正方向,![]() 为单位长,打造如图所示的空间直角坐标系D-xyz,
为单位长,打造如图所示的空间直角坐标系D-xyz,
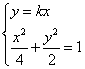
则C(0,1,0),B(1,1,0),![]() (0,1,2),E(1,0,1),
(0,1,2),E(1,0,1),![]() ,
,![]() .
.
设平面EBC的法向量为n=(x,y,x),则
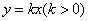 即
即![]()
所以可取n=![]() .
.
设平面![]() 的法向量为m=(x,y,z),则
的法向量为m=(x,y,z),则
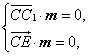 即
即![]()
所以可取m=(1,1,0).
于是![]() .
.
所以,二面角![]() 的正弦值为
的正弦值为![]() .
.
18.解:(1)X=2就是10:10平后,两人又打了2个球该局比赛结束,则这2个球均由甲得分,或者均由乙得分.因此P(X=2)=0.5×0.4+(1–0.5)×(1–04)=05.
(2)X=4且甲获胜,就是10:10平后,两人又打了4个球该局比赛结束,且这4个球的得分状况为:前两球是甲、乙各得1分,后两球均为甲得分.
因此所求概率为
[0.5×(1–0.4)+(1–0.5)×0.4]×0.5×0.4=0.1.
19.解:(1)由题设得![]() ,即
,即![]() .
.
又由于a1+b1=l,所以![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
由题设得![]() ,
,
即![]() .
.
又由于a1–b1=l,所以![]() 是首项为1,公差为2的等差数列.
是首项为1,公差为2的等差数列.
(2)由(1)知,![]() ,
,![]() .
.
所以![]() ,
,
![]() .
.
20.解:(1)f(x)的概念域为(0,1),(1,+∞)单调递增.
由于f(e)=![]() ,
,![]() ,
,
所以f(x)在(1,+∞)有唯一零点x1,即f(x1)=0.
又![]() ,
,![]() ,
,
故f(x)在(0,1)有唯一零点![]() .
.
综上,f(x)有且仅有两个零点.
(2)由于![]() ,故点B(–lnx0,
,故点B(–lnx0,![]() )在曲线y=ex上.
)在曲线y=ex上.
由题设知![]() ,即
,即![]() ,
,
故直线AB的斜率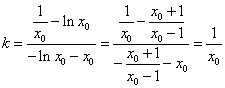 .
.
曲线y=ex在点![]() 处切线的斜率是
处切线的斜率是![]() ,曲线
,曲线![]() 在点
在点![]() 处切线的斜率也是
处切线的斜率也是![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线也是曲线y=ex的切线.
处的切线也是曲线y=ex的切线.
21.解:(1)由题设得![]() ,化简得
,化简得![]() ,所以C为中心在坐标原点,焦点在x轴上的椭圆,不含左右顶点.
,所以C为中心在坐标原点,焦点在x轴上的椭圆,不含左右顶点.
(2)(i)设直线PQ的斜率为k,则其方程为![]() .
.
由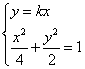 得
得![]() .
.
记![]() ,则
,则![]() .
.
于是直线![]() 的斜率为
的斜率为![]() ,方程为
,方程为![]() .
.
由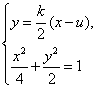 得
得
![]() .①
.①
设![]() ,则
,则![]() 和
和![]() 是方程①的解,故
是方程①的解,故![]() ,由此得
,由此得![]() .
.
从而直线![]() 的斜率为
的斜率为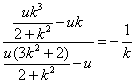 .
.
所以![]() ,即
,即![]() 是直角三角形.
是直角三角形.
(ii)由(i)得![]() ,
,![]() ,
,
所以△PQG的面积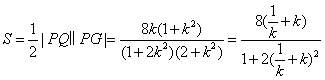 .
.
设t=k+![]() ,则由k>0得t≥2,当且仅当k=1时取等号.
,则由k>0得t≥2,当且仅当k=1时取等号.
由于![]() 在[2,+∞)单调递减,所以当t=2,即k=1时,S获得最大值,最大值为
在[2,+∞)单调递减,所以当t=2,即k=1时,S获得最大值,最大值为![]() .
.
因此,△PQG面积的最大值为![]() .
.
22.解:(1)由于![]() 在C上,当
在C上,当![]() 时,
时,![]() .
.
由已知得![]() .
.
设![]() 为l上除P的任意一点.在
为l上除P的任意一点.在![]() 中
中![]() ,
,
经检验,点![]() 在曲线
在曲线![]() 上.
上.
所以,l的极坐标方程为![]() .
.
(2)设![]() ,在
,在![]() 中,
中,![]() 即
即![]() ..
..
由于P在线段OM上,且![]() ,故
,故![]() 的取值范围是
的取值范围是![]() .
.
所以,P点轨迹的极坐标方程为![]() .
.
23.解:(1)当a=1时,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,不等式![]() 的解集为
的解集为![]() .
.
(2)由于![]() ,所以
,所以![]() .
.
当![]() ,
,![]() 时,
时,![]()
所以,![]() 的取值范围是
的取值范围是![]() .
.







